数量关系 | 国家公务员招录考试

数学运算

计算问题

算式计算

常用法则	具体公式
加法	$ a+b=b+a，(a+b)+c=a+(b+c) $
乘法	$ a\times{b}=b\times{a}，(a\times{b})\times{c}=a\times{(b\times{c})} $
幂次	$ a^{m}\times{a^{n}}=a^{n}\times{a^{m}}=a^{m+n}，(a^m)^n=(a^n)^m=a^{mn}，(a\times{b})^m=a^m\times{b^m}，(\frac ba)^m=\frac {b^m} {a^m} $
完全平方公式	$ (a\pm b)^2=a^2\pm 2ab+b^2 $
平方差公式	$ a^2-b^2=(a+b)(a-b) $
完全立方公式	$ (a\pm b)^3 = a^3\pm 3a^2b+3ab^2+b^3 $
立方和(差公式)	$ a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2) $
列项公式	$ \frac {d} {n(n+d)}=\frac 1n - \frac{1}{n+d}，当d=1时，\frac{1}{n(n+1)}=\frac 1n-\frac{1}{n+1} $

数列计算

数列	通项公式	对称公式	求和公式
等差数列	$a_n=a_1+(n-1)d$	$a_m+a_n=a_i+a_j，其中m+n=n+j$	$①一般求和：S_n=\frac {n(a_1+a_n)} {2}=na_1+\frac 12n(n-1)d \\ ②中项求和：S_n=\begin{cases} na_{\frac{n+1}{2}} ，n为奇数 \\ \frac n2(a_{\frac n2}+a_{\frac n2 + 1}) ，n为偶数 \end{cases}$
等比数列	$a_n=a_1·q^{n-1}$	$a_m·a_n=a_i·a_j，其中 m+n=i+j$	$S_n=\begin{cases} \frac{a_1(1-q^n)}{1-q}，q \neq 1 \\ na_1，q = 1 \end{cases}$
平方数列	$a_n=n^2$		$S_n=\frac 16 n(n+1)(2n+1)$
立方数列	$a_n=n^3$		$S_n=[\frac 12 n(n+1)]^2$

• 平方数列利用 $(n+1)^3-n^3=3n^2+3n+1$ 多项式求和
• 立方数列利用 $(n+1)^4-n4=4n^3+6n^2+4n+1$ 多项式求和

平均数与均值不等式

分类	概念及公式
算术平均数	所有数据之和除以数据个数所得的商，用公式表示为 $ M=\frac {m_1+m_2+m_3+ \cdots +m_n}{n} $
加权平均数	比重不同的一组数据的平均数，即把原始数据按照合理的比例来计算。 在一组数据中，$ x_1、x_2、x_3、\cdots、x_k $ 出现的次数分别为 $ f_1、f_2、f_3、\cdots、f_k $ ， 且 $ f_1+f_2+f_3+ \cdots +f_k=n $， 那么这组数据的加权平均数 $ \overline X = \frac {x_1 \cdot f_1 + x_2 \cdot f_2 + \cdots + x_k \cdot f_k} {f_1+f_2+f_3+ \cdots +f_k} = \frac {x_1 \cdot f_1 + x_2 \cdot f_2 + \cdots + x_k \cdot f_k} {n} $
几何平均数	几个正实数乘积的n次算术根，用公式表示为 $ G=\sqrt[n]{m_1 \cdot m_2 \cdot m_c \cdot \cdots \cdot m_n} $
圴值不等式	任意几个正数的算术平均数总是不小于其几何平均数。即 $ \frac {m_1+m_2+m_3+ \cdots +m_n}{n} \geqslant \sqrt [n] {m_1 \cdot m_2 \cdot m_c \cdot \cdots \cdot m_n} $ ，当且仅当 $ m_1=m_2=m_3= \cdots =m_n $ 时，等号成立。

• 公务员考试多考查两个数或三个数的均值不等式：

$ ① \frac {a+b}{2} \geqslant \sqrt{ab}，当且仅当 a=b 时等号成立；$

$ ② \frac {a+b+c}{2} \geqslant \sqrt[3]{abc}，当且仅当 a=b=c 时等号成立。$

比较大小

常用的比较大小的方法有作差法、作商法、倒数法和中间值法。

定义新运算

解定义新运算问题，只需将新定义的运算规则转化为常规的四则运算即可。

和差倍比问题

和差倍问题

和差倍问题的解题关键在于“1倍量”的计算，考生要正确理解题意。情况比较复杂时，可采用方程 法简化思路。

和差倍问题可分为如下三类：

比例问题

核心公式：分量 ÷ 总量 = 所占比例、分量 ÷ 所占比例 = 总量。

解题关键：比例问题的解题关键是找准各分量、总量及两者之间的比例关系。当题干涉及两个数的比，日这两个数必须为整数时。可运用数字特征对选项进行筛选，即排除法。分数、百分数皆适用。

连比问题

在数学运算中，连比问题的题干多是给出三个已知量中任意两个比例式，可通过对两个比例式的转化得到三个量的比例关系。

解题关键：连比问题可通过找最小公倍数，直接确定答案。

行程问题

• 行程问题的研究核心是物体运动过程中速度、时间和路程三者之间的关系。

行程问题的基础知识

核心公式：路程=时间x速度。

比例关系：时间相同，速度比=路程比；速度相同，时间比=路程比； 路程相同，速度比=时间反比。

平均速度：平均速度=总路程÷总时间。

若物体前一半时间以速度$v_1$运动，后一半时间以速度$v_2$运动，则全程的平均速度为$\frac {v_1+v_2}{2}$

若物体前一半路程以速度$v_1$运动，后一半路程以$v_2$运动，则全程的平均速度为$\frac {2v_1v_2}{v_1+v_2}$

行程问题的基本类型

常见的行程问题核心考点及相关公式如下表所示：

问题类型	核心考点及相关公式
相遇问题	相遇问题主要研究两个物体相向(相对)运动的情况 相遇时间=相遇路程÷速度和
追及向题	追及问题主要研究两个物体同向运动的情况 追及时间=追及路程÷速度差
往返多次相遇问题	从两地同时出发的直线多次相遇问题中，第 n 次相遇时，每个人走的路程等于他第一次相遇时所走路程的 (2n-1) 倍
环线相遇问题	环线相遇向题中每次相遇所走的路程之和是一圈。如果最初从同一点出发，那么第 n 次相遇时，每个人所走的总路程等于第一次相遇时所走路程的 n 倍
环线追及问题	环线追及问题中每次相遇所走的路程差是一圈。如果最初从周长为 S 的环形跑道同一点出发，那么第 n 次相遇时，两个人的路程差为 nS
流水问题	流水问题主要是研究船在逆水和顺水时的速度差别 顺水速度=船速＋水速；逆水速度=船速-水速 船速=(顺水速度＋逆水速度)÷2；水速=(顺水速度-逆水速度)÷2
火车过桥问题	火车在运动过程中，在计算火车走过的路程时，需要将”车长“考虑进来 火车速度x时间=车长+桥长

工程问题

• 工程问题中涉及工作量、工作时间和工作效率三个量，其核心公式是工作量=工作效率x工作时间。常见的工程问题如下所示

• 水管问题属于工程问题的衍生。当遇到注水问题时，可将注水管的工作效辛视为正，排水管的工作效率视为负；遇到排水问题时，注水管的工作效率为负，排水管的工作效率为正。

浓度问题

• 浓度问题指与溶液浓度相关的问题。题型可分为两种，溶液蒸发或稀释问题以及两种溶液的混合问题，

基本概念

• 溶剂：溶剂是一种可以溶化固体、液体或气体的物质。日常生活中比较常见的溶剂一般为液体。例如盐水溶液中的水就是溶剂。
• 溶质：溶质是溶液中被溶剂溶解的物质。例如盐水溶液中的食盐就是溶质。
• 溶液：溶液是由溶质和溶剂共同组成的混合物。例如食盐溶于水形成的混合物为盐水溶液。
• 浓度：我们日常生活以及公务员考试中所涉及的浓度一般指的是质量百分浓度，即溶液中所含溶质质量与溶液质量的百分比。

基本公式

• 溶液质量=溶质质量+溶剂质量
• 浓度=溶质质量-溶液质量×100%

溶液的混合特性

• 一种高浓度的溶液 A 和一种低浓度的同种溶液 C 混合后得到溶液 B，那么溶液 B 的溶度肯定介于溶液 A 和溶液 C 的浓度之间。

利润问题

概念及相关公式

利润问题相关概念及公式如下所示：

概念	含义	示例	相关公式
进价	商品买进的价格	商家以每件 100 元买人某商品
定价	商家根据进价定出的商品出售价格	商家决定以每件 150 元卖出某商品
售价	商品实际的出售价格	商家实际以每件 120 元卖出某商品
利润	售价与进价的差	每件商品商家赚了 120-100=20 元	利润=售价-进价
利润率	利润占进价的百分比	利润率为 20÷100=20%	$利润率= \frac {利润}{进价} $

主要题型

• 简单获利问题：题目内容都与进价、售价和利润有关，主要利用相关公式解决问题。
• 打折问题：商家确定价格之后，为吸引更多顾客购买商品，通常采用打折的方式降低实际价格。
• 价格与销量反向变化问题：当商品价格上涨时，销量就会下降；价格下跌时，销量就会增加。在公务员考试中，研究此类问题，一般是求总利润最高时的售价或总利润的最大值
• 多种促销问题：商家有时会给出多种促销方式，我们需要通过计算，确定最优惠的促销方式。

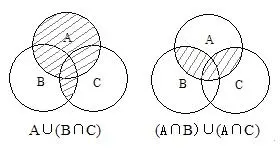
容斥问题

• 几个集合之间存在交叉关系 ，要求根据其相互关系计算元素个数的问题称为“容斥原理”问题。公务员考试中，多涉及两个集合或三个集合。
• 容斥问题的常用解题方法有公式法和文氏图法两种。

公式法

• 两个集合：$A \cup B = A+B-A \cap B$
• 三个集合：$A \cup B \cup C=A+B+C-A \cap B-B \cap C-C \cap A+A \cap B \cap C$
  注意：计算时要找准集合的对应关系及公式中各项的对应数值

文氏图法

当题目关系较为复杂时，可考虑画文氏图，帮助看清各集合之问的关系。如下所示：

抽屉问题

时钟问题

钟面问题

• 钟面问题主要研究钟面上时针与分针的关系，通常围绕时针与分针重合、垂直、成直线、呈多少度角提出问题。
• 钟面的1圈为60格，时针每小时走 5 格，即 30°，每分钟走 $\frac {1}{12} $ 一格，即 0.5°。
• 分针每小时走 1 圈，即 360°；每分钟走 1 格，即 6°。
• 时针与分针的速度之差为 5.5 度/分。
  解题关键: 确定分针与时针的初始位置，得出两者的路程差

坏钟问题

• 涉及坏钟时间与标准时间的问题，统称为坏钟问题。
• 坏钟问题的本质是比例问题，解题时只需我出坏钟时间与标淮时间的倍比关系即可。每小时快 N 分钟，则标淮时间的 1 小时即 60 分钟里，快钟走(60+N)分钟，快钟时间:标淮时同=(60+N):60。

分段计价问题

分段计价是指按照不同的等级标淮，收取费用或进行利润分配。

解题关键： 解决分段计价问题，关键是要弄清分界点，而后再分区间进行计算。情况复杂时可考虑 边界情况，帮助分析。解题过程中一般需要利用不定方程和数的特性，对选项进行合理地判断以提高计算效率。

年龄问题

年龄问题主要考查多人之间的年龄变化情况，其核心是“年龄差不变”。

年龄问题的三大规律

年龄问题的三大规律为：①两人的年龄差是不变的；②两人年龄的倍数关系是变化的；③随着时间的推移，两人年龄的增加量相等

常用解题方法

年龄问题常用解题方法包括：①方程法；②利用和差倍关系；③代入排除法。

日期问题

日期问题是指根据已知条件求具体日期或者星期的一类问题。其主要知识点如下所示：

知识点	判断方法	一年总天数	2月天数
闰年	非100的倍数，能被 4整除 100的倍效，能被 400整除	366	29
平年	不是闰年，则为平年	365	28

星期每7天一循环。平年星期数加1，闰年星期数加 2(其间包含2月29日)

植树问题

在给定的一段路线上等距离植树，同时给出植树的方式、相邻两树之间的距离或路的总长度等，要求求出共需要种至少多少棵树。这是植树问题常见的提问方式。

植树问题中经常涉及的概念有总路长、间距和棵数。

基本类型

植树问题基本类型及其公式如下所示：

问题类型	公式
路不封闭且两端都植树	棵数=总路长÷间距+1
路不封闭且有一端植树	棵数=总路长÷间距
封闭道路植树(闭合曲线)	棵数=总路长÷间距
路不封闭且两端都不植树	棵数=总路长÷间距-1

典型变形

围绕植树问题的核心概念———— 总路长、间距和棵数之间的相互关系，还可以对植树问题的题目背景进行拓展变形，衍生出下面四种题型

锯木头问题

一根木料有两个端点，n 段有 2n 个端点，每锯一次增加两个端点。故一根木料要锯成 x 段，需要增加(2x-2)个端点，即只需锯(x-1)次，相当于两端不植树的不封闭植树问题

爬楼梯问题

一幢 n 层的高楼，从底层到顶层需要走(n-1)层的楼梯，相当于两端都植树的不封闭植树问题。若爬完一层休息一次，则从底层到顶层需要休息(n-2)次。

打木桩问题

一段路打了 n 个木桩，每一根木桩就相当于一棵树，一般来说，木桩要求在路的两端都要打上一根，因此，打木桩问题就相当于两端都植树的不封闭植树问题。

队列问题

一列队伍中，每列(行)有 n 人，则中间有(n-1)个间距。若间距为 a 米，则队伍长为 a(n-1) 米，相当于两端都植树的不封闭植树问题。

方阵问题

方阵问题是指许多人或物按一定条件排成正方形(方阵)，需要根据方阵找出规律，进而解决问题。在解决问题时，首先要搞清方阵中的一些量(如层数、最外层人数、最里层人数、总人数)之间的关系，再选择方阵问题中常用的公式及性质。

方阵问题的四个规律：

方阵相邻两层人数相差8(此处需注意一种特殊情况，当实心方阵的最外层每边人数为奇数时，从内到外每层人数依次是 1、8、16、24……)。

实心方阵总人数=最外层每边人数的平方(核心公式)；空心方阵总人数利用等差数列求和公式求解(首项为最外层总人数，公差为-8)。

方阵每层总人数=方阵每层每边人数x4-4。

在方阵中若去掉一行一列，去掉的人数 = 原来每行人数x2-1； 在方阵中若去掉二行二列，去掉的人数 = 原来每行人数×4 - 2x2。

盈亏问题

盈亏问题的常见形式为给出某物体的两种分配标准和结果，求物体和分配对象的数量。由于每次分配可能出现刚好分完、多余或不足三种情况，所以会出现多种结果的组合。

盈亏问题常见问题类型及其公式如下所示：

问题类型	公式
一盈一尽型	盈数÷两次分配个数的差=对象数
一亏一尽型	亏数÷两次分配个数的差=对象数
一盈一亏型	(盈数＋亏数) ÷ 两次分配个数的差=对象数
两次皆盈型	(大盈数-小盈数) ÷ 两次分配个数的差=对象数
两次皆亏型	(大亏数-小亏数) ÷ 两次分配个数的差=对象数

由上述公式可知，解决盈亏问题的关键是利用公式求出分配的对象数，再求出物资数。

公务员考试中常出现的是一盈一亏型。

鸡兔同笼问题

在鸡兔同笼问题中，如果要求其中一种物品的数量，一般采用假设法，即“设鸡求免”。
在公考员考试中经常出现的“得失“问题，也可看作鸡兔同笼问题，利用假设法求解。具体解题方法如下所示：

标准鸡兔同笼问题	鸡免同笼问题变形题
设鸡求兔	设得求失
兔头数=(总脚数-2x总头数)÷2 鸡头数=总头数-免头数	损失数=(每件应得x总件数-实得数)-(每件应得+每件损赔)

除此之外，也可以用方程法解决此类问题。只需分别设出两种物品的数量，列二元一次方程组即可。

牛吃草问题

解牛吃草问题的一般流程如下：

几何问题

几何问题一般涉及几何图形的周长、面积、角度、表面积与体积等。最常见的形式是给出一个具体图形，直接计算某一个量。一般来说，几何图形的基本公式是解决几何问题的关键。

1. 几何问题核心公式

(1) n 边形内角和公式

n 边形内角和为(n-2)×180°。

(2)平面图形

常见平面图形的周长及面积公式如下所示：

图形	图例	周长	面积
三角形	?	$C=a+b+c$	$S_{\triangle ABC}= \frac 12 ah \\ S_{\triangle ABC}=\frac 12ab \sin C = \frac 12 ac \sin B = \frac 12 bc\sin A$
正方形	?	$C=4a$	$S=a^2$
长方形	?	$C=2 (a+b)$	$S=ab$
梯形	?	-	$S= \frac 12(a+b)h$
平行四边形	?	-	$S=ah$
圆形	?	$C=2 \pi r= \pi d$	$S= \pi r^2 = \frac 14 \pi d^2 $
扇形	?	$C=( 2 + \frac {n°} {180°} \pi )r$	$ S = \frac {n°} {360°} \pi r^2$

(3)立体图形

常见立体图形的表面积及体积公式如下所示：

图形	图例	表面积	体积
长方体	?	$S=2 (ab+bc+ac)$	$V=abc$
正方体	?	$S=6a^2$	$V=a^3$
球体	?	$S=4 \pi r^2$	$V= \frac 43 \pi r^3$
圆柱体	?	$S=2 \pi r^2 +2 \pi rh$	$V=Sh=\pi r^2h \\ (S为圆柱底面积)$
圆锥体	?	-	$V=\frac 13Sh=\frac 13 \pi r^2h \\ (S为圆锥底面积)$

2.一般解题过程中的常用结论

(1)极限理论

• 平面图形：①周长一定，越趋近于圆，面积越大；②面积一定，越趋近于圆，周长越小。
• 立体图形：①表面积一定，越趋近于球，体积越大；②体积一定，越趋近于球，表面积越小。

(2)三角形的常见考点

三角形的常见考点包括，①两边之和大于第三边，两边之差小于第三边；②较小的角对应边也较小。

排列组合与概率问题

1.排列组合

(1)两个基本原理

排列组合的两个基本原理如下所示：

• 分类用加法原理：$m_1 + m_2 + \dots + m_n$
• 分步用乘法原理：$m_1 × m_2 × \dots × m_n$

(2)三个原则

排列组合的三个原则包括：①特殊元素优先考虑；②复杂问题从对立面考虑；③环形问题转化为直线问题

(3)四个方法

• 捆绑法：n 个不同元素排成一列，要求 m 个元素必须相邻，可以把 m 个元素看成一个整体，此时有 $A_{n-m+1}^{n-m+1}A_m^m$ 种排法。
• 插空法：n 个不同元素排成一列，要求 m 个元素互不相邻，可以先排好其余的(n-m)个元素，然后将 m 个元素插到(n-m)个元素形成的(n-m+1)个空之间，有 $A_{n-m}^{n-m}A_{n-m+1}^m$ 种排法。
• 插板法：将 n 个相同元素分成 m 堆，每堆至少一个，相当于将 (m-1) 个木板插到 n 个元素形成的(n-1) 个“空”中，有 $C_{n-1}^{m-1}$ 种分法。
• 归一法：n 个不同元素排成一列，其中 m 个元素的位置相对确定，如甲必须在乙前面等，此时将所有元素正常全排列，然后除以 m 个元素的全排列数即可，此时有 $\frac {A_n^n} {A_m^m} = \frac {n!} {m!}$ 种排法。

以上几种方法的针对性很强，只能够解决某一种排列组合问题，但是这些问题正好就是公务员考试中的重点题型。

(4)两个经典模型

• 错位重排：错位重排问题是指把 n 个元素的位置重新排列，使每个元素都不在原来的位置上的排列问题。记 n 个元素错位重排数为 $D_n$ ，则 $D_n=(n-1)(D_{n-1}+D_{n-2})，D_1=0，D_2=1，D_3=2$。
• 环线排列：环线上的排列问题没有前后与首尾之分，任取一个元素作为队首，环线排列问题便转化为剩下 (n-1) 个元素的直线排列问题，不同的排列方式有 $A_{n-1}^{n-1} = (n-1)!$ 种

2. 概率问题

常见的概念问题类型及其概念、公式如下所示：

分类	概念及公式
古典概率	将所有情况分成 n 个等可能的情形，其中事件 A 包括了 m 个情形，那么事件 A 发生的概率为 $\frac mn，记为 P(A)$
条件概率	事件 A 在另外一个事件 B 己经发生的条件下的发生概率，记为 P(A | B) P(A | B)=$\frac {P(A B)}{P(B)}$ P(AB)为AB同时发生的概率，P(B) 为 B 发生的概率
独立重复试验概率	如果在一次试验中事件 A 发生的概率为p，在 n 次独立重复试验中，事件 A 发生 k 次的概率为 P(k) = $C_n^kp^k(1-p)^{n-k}$

统筹问题

统筹问题的本质就是在众多利用人力、物力资源的方案中，选择一个最优的万案，使工作效率达到最高。此类问题是最为贴近实际生活的，需要具体问题具体分析。题型主要可分为以下几类：

题型分类	解题方法
时间安排问题	关键：找出能同时进行的任务，缩短工作时间
排队问题	关键：找出能同时进行的任务，缩短工作时间
空瓶换酒问题	核心公式：$C= /frac {B}{A-1}，A 代表 A 个空瓶可以换 1 瓶酒，B =空瓶数，C 代表通过空瓶换酒能喝到多少瓶酒
物资集中问题	本质:判断货物流通的方向。常用方法为判断每条“路”两侧的货物总重量，在这条“路”上一定是从轻的一侧流向重的一侧(只适用于非闭合路径中)
货物装卸问题	结论：如果有 M 辆车和 N(N>M) 个工厂，所需装卸工的总数就是需要装卸工人数最多的M个工厂所需装卸工人数之和(若 M $\geqslant$ N ，则跟车人数为 0，各点需要工人数之和即答案)
策略制定问题	实质：利用数学工具或数学思维有规划地安排工作内容及流程，使人力、物力、时间、金钱等得到合理的利用，确保使用最少的资源达到最高的效率

推理问题

推理问题主要考查应试者的基本逻辑推理能力。考生依据题干条件进行步骤推理，以而对数学运算中的数量关系进行限定，最终得出结论。随着公务员考试对考生思维过程考查的力度加大，推理问题出现的频率越来越高，难度也有所加大。常见的推理问题题型及解题思路如下所示：

题型	解题思路
利用逻辑知识推理	考生需具备清哳的推理思维能力，与逻辑判断题类似，但需要进行简单的计算
利用整数性质推理	题干通常给出若干个不同的整数，利用整数的相关性质(如奇偶性、整除性)，结合题干中的信息进行推理分析
利用最值思想推理	通过计算，从最差或最好的情况出发，进行推理
利用不定方程推理	根据题干的数量关系列出不定方程，再通过限制条件求解

数学推理

等差数列及其变式

如果一个数列从第二项起，每一项与前一项的差等于同一个常数，那么，该数列就叫作等差数列。等差数列的变化形式如下图所示

等比数列及其变式

如果一个数列从第二项起，每一项与它前面一项的比等于同一个非0常数，那么该数列就叫作等比数列。等比数列的主要变化形式如下图所示：

• 基本等比数列 (后一项÷前一项)
  • 常数
• 等比数列变式 (后一项÷前一项)
  • 等比数列、等差数列、多次方数列、和数列、质数列、循环数列……
  • 前一项x常数+常数=后一项
    前一项x常数+基本数列=后一项
    前一项x基本数列+常数=后一项
    前一项x基本数列+基本数列=后一项
    _

和数列及其变式

和数列及其变式指通过作和寻求规律的数列。

1.典型和数列

• 两项和数列：从第三项起，每一项等于它前面两项之和。
• 三项和数列：从第四项起，每一项等于它前面三项之和。
• 拓展：每一项等于它前面所有项之和。

2.和数列变式

和数列变式根据变化方式的不同，主要分成以下三类。

• 和数列变式分类
  • 相邻两项依次求和，得到基本数列或变式
    • 求和得到等差数列、等比数列、多次方数列、质数列。
  • 相邻两项求和后经过简单变化，得到第三项。
    • 第一项+第二项+常数=第三项
      第一项+第二项+基本数列=第三项
      (第一项+第三项)x常数=第三项
      (第一项+第二项)x基本数列=第三项
      _
  • 相邻两项简单变化后求和。得到第三项
    • 第一项+第二项x常数=第三项
      第一项x常数+第二项=第三项
      第一项x常数＋第二项x常数=第三项
      第一项x基本数列+第二项x基本数列=第三项
      _

积数列及其变式

积数列及其变式是指项与项间通过作积呈现出一定规律的数列。其主要变化形式如下图所示：

• 积数列基本形式
  • 三项积数列
    • 每一项等于前三项相乘
  • 两项积数列
    • 每一项等于前两项相爽
• 积数列变式
  • 相邻两项依次求积，得到基本数列
  • 相邻两项求积之后，经过简单变化得到第三项

多次方数列及其变式

数列呈现多次方数，且底数、指数各自具有规律，称为多次方数列；在此基础上经过简单运算得到的数列，为多次方数列变式。它们的主要规律如下表所示：

分类	规律	示例
多次方数列基本形式	平方数列：数列逐项可以改写为平方数，底数呈现规律	数列 1，4，9，16，可以改写为 $1^2，2^2，3^2，4^2$
多次方数列基本形式	立方数列：数列逐项可以改写为立方数，底数呈现规律	数列 1，8，27，64，可以改写为 $1^3，2^3，3^3，4^3$
多次方数列基本形式	多次方数列：数列各项可改写成指数、底数均不相同的数列，底数和指数分别具有规律	数列 0，1，8，81，可以改写为 $0^1，1^2，2^3，3^4$
多次方数列变式	对数列各项进行多次方改写，并加入常数做简单运算得到原数列	数列 2，5，10，17，经过换算后为 $1^2+1，2^2+1，3^2+1，4^2+1$
多次方数列变式	数列各项之间通过幂次运算形成递推规律	数列 2，3，11，38，规律为第一项的立方+第一项=第三项即 $2^3+3=11，3^3+11=38$

分式数列

  分式数列是指题干以分数为主的数列。由于分数本身可以进行通分和约分，所以分子、分母具有多变性，这也是分式数列规律难以寻找的主要原因。
  分式数列最基本的表现形式是数列本身可以构成基本数列或其变式。
  在公务员考试中，分式数列的考查重点是按其内在变化规律分为两类：一种是分子分母分别变化型；另一种是分子分母关联变化型。其具体变化规律如下表所示：

规律变化类型	举例说明
分子分母分别变化型	$数列各项的分子、分母分别组成基本数列或其变式 \\ 例如： \frac 21，\frac 64，\frac {10}{9}，\frac {14}{16}，\frac {18}{25}$
分子分母关联变化型	$依次变化型：将数列各项的分子分母依次排列，得到一个基本数列或其变式 \\ 例如：数列\frac 12，\frac 34，\frac 56，\frac 78 分子分母依次排列得到自然然数列1，2，3，4，5，6，7，8$
分子分母关联变化型	$交错变化型：两个基本数列在各项分子、分母位置交错排列 \\ 例如：数列 \frac 11，\frac 34，\frac 95，\frac {7}{16}，\frac {25}{9}，\frac {11}{36} \begin{cases} 公差为2的等差数列 \\ 平方数列 \end{cases}$
分子分母关联变化型	$递推变化型：数列各项的分子(或分母)都是前一项分子、分母简单运算的结果，\\ 有时也涉及本项的分母(或分子) \\ 例如：数列各项依次是 \frac 11，\frac 24，\frac {6}{11}，\frac{17}{29}，\frac{46}{76}，\frac {122}{199} \\ 每一项的分子等于前一项的分子与分母的和，46+76=(122) \\ 每一项的分母等于该项的分子加前一项的分母再加 1，76+122+1=(199)。\\ 或分母依次是 1，4，11，29，76，(199)，满足第二项x3-第一项=第三项，\\ 依此类推，所填分数的分母为 76×3-29=(199)$

组合数列

与之前所讲的等差数列、等比数列、和数列、积数列不同，组合数列的侧重点是考查数列结构特征，只要考生发现了数列的结构特征，就能找到推理规律，组合数列主要分为以下三类：

分类	特点
间隔组合数列	数列的奇数项和偶数项分别构成某个基本数列或其变式
分组组合数列	数列相邻数宇可分成独立的几组，组内数字或组间数字在运算关系上存在一定的联系
数位组合数列	数位对应型数列：各项相同数位上的数字组成一个简单数列
数位组合数列	数位关系型数列：每项分成几个部分，构成运算关系，各项彼此之间存相同或相似的联系

创新数列

除去以上介绍的数字推理中各类常考的基本数列及其变式，随着数字推理题型的发展和创新。又出现了很多新颖的数字推理规律。归纳总结，大致可按以下几个方面分类：

• 创新数列
  • 质数列
    • 质数(或合数)按某种规律排列位置
  • 数字和(数字积)
    • 各项数字和(或数字积)相等或组成简单基本数列
  • 数字排序
    • 数项各位数字按一定规律排列
  • 运算关系
    • 类似于递推数字规律，但运算方式更加新颖、复杂
  • 其他形式

图形形式数字推理

图形形式数字推理是指数字分布在图形中，由于位置不同而具有相应的运算关系。按图形形状可分为以下几类：9

分类	表现形式	核心本质
圆圈形式	四个数字分布在一个被四等分的圆中	按纵、横、斜向(对角线)三种方式对数字进行分组，通过运算使两组数的结果相等
圆圈形式	在简单圆圈形式的基础上在中心增加一个数字	四周的数字通过简单运算得到中间的数字
表格形式	数字在表格之中，多为九宫格样式	同九宫格形式的图形推理类似，运算规律多，集中在行列间，有时也表现为整体规律
表格形式	带中心数宇圆圈形式数字推理的变形	同带中心数字的圆圈形式数字推理一致
三角形式	带中心数字圆圈形式的简化，三角形的三个角各有一个数字，中间有一个数字	三个角的数字通过运算得到中间数宇
其他图形形式	各种图形的变形、简化	均需要通过构造运算规律，得到等量关系